
Maps are amazing tools. They help us understand the world around us, find our way, and even learn about the shape of our planet. But making maps is not as easy as it might seem. That’s because the Earth is round (like a ball), and maps are flat. Turning a round object into a flat picture takes some clever thinking and a lot of math. In this guide, we’ll explore the mathematics behind maps of the Earth in a simple and easy-to-understand way.
We will look at six important ideas:
- The Hunter and the Bear
- Metric Spaces
- Spherical Geometry
- Projections
- Hyperbolic Geometry
- Topology
1. The Hunter and the Bear
Let’s start with a riddle:
"A hunter walks 1 mile south, 1 mile east, and 1 mile north. He ends up at the same spot he started. What color is the bear?"
The answer is: white. Why? Because the hunter must be near the North Pole, and the only bears that live there are polar bears, which are white.
But what does this have to do with math? This riddle is actually a clever way to talk about the shape of the Earth and how directions work on a sphere. On a flat surface, walking south, then east, then north would never bring you back to the same place. But on a round Earth, it’s possible. This shows us that the usual rules of geometry change when we move from flat to curved surfaces.
2. Metric Spaces
Before we go further, we need to understand something called a metric space. Don’t worry, it sounds more complicated than it is.
A metric space is just a set of points with a rule to measure distance between them. For example, on flat paper, the distance between two points is the straight line between them. But on a curved surface like the Earth, the shortest path between two points is not a straight line—it’s a curve called a geodesic.
Think of a globe. If you draw a line from New York to London, the shortest path curves across the top of the globe. That curved line is a geodesic.
Metric spaces help us understand different kinds of surfaces and how to measure distances on them. This idea is important when making maps because we need to compare distances on Earth with distances on paper.
3. Spherical Geometry
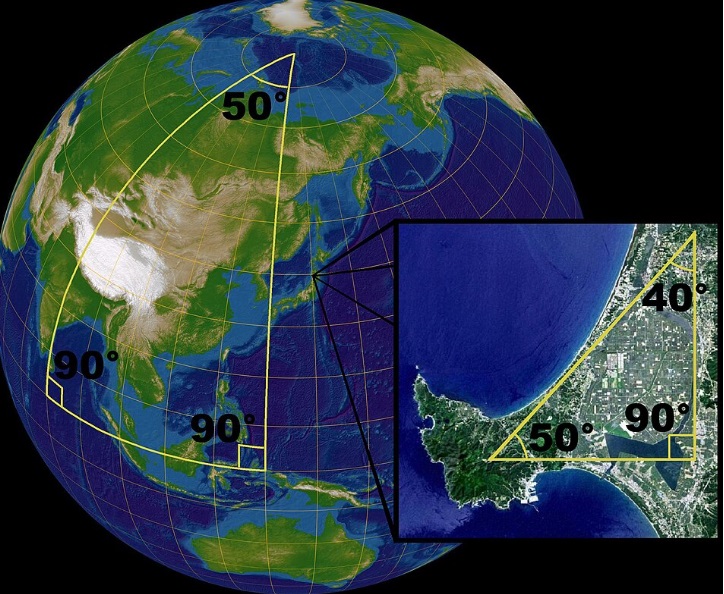
Since the Earth is (almost) a sphere, it follows the rules of spherical geometry. This is a kind of geometry used on curved surfaces like globes.
In spherical geometry:
- Straight lines become great circles (like the equator or lines of longitude).
- The sum of the angles of a triangle is more than 180 degrees.
- There are no parallel lines, because all great circles eventually meet.
This is very different from the flat geometry we learn in school, called Euclidean geometry. Spherical geometry is key to understanding how maps are made, because it tells us how shapes and distances really work on a round planet.
4. Projections
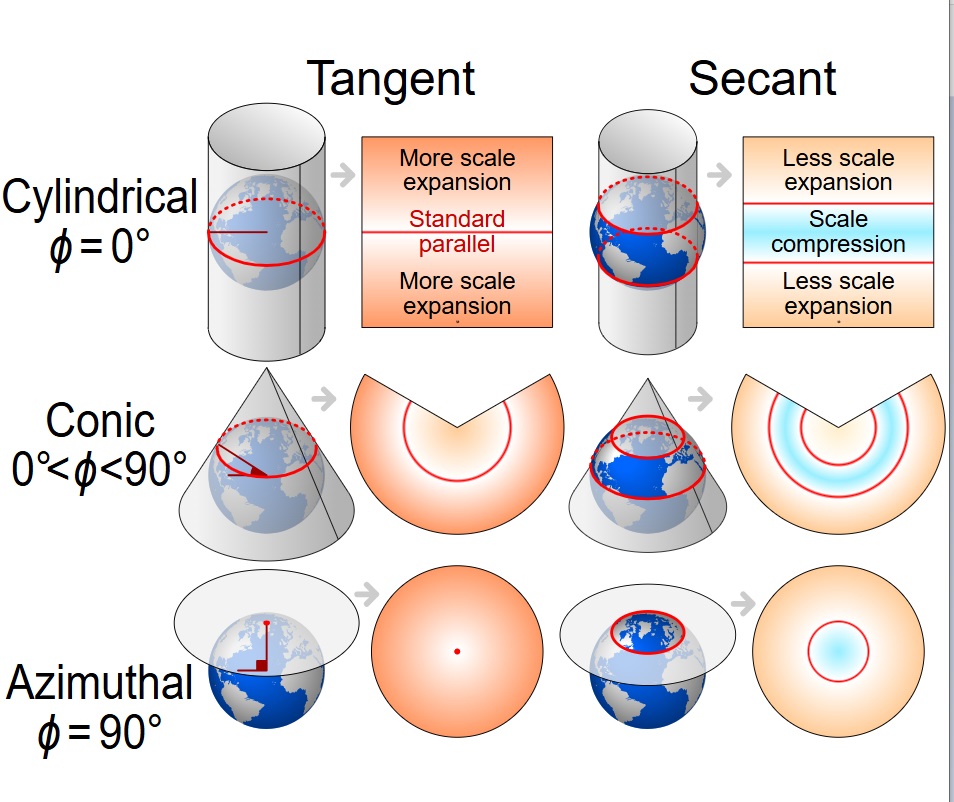
Now here’s the big challenge: how do we take the curved surface of the Earth and flatten it into a map?
This is where map projections come in. A projection is a method of turning the round Earth into a flat image. But there’s a catch: you can’t do it perfectly.
Every projection has to make a trade-off. It can preserve:
- Distances (but shapes get distorted)
- Shapes (but areas get distorted)
- Areas (but angles or distances get distorted)
Some common projections include:
- Mercator Projection: Good for navigation, because it keeps angles and shapes correct near the equator. But it makes places near the poles (like Greenland) look much larger than they really are.
- Peters Projection: Shows areas more accurately, but stretches shapes.
- Robinson Projection: A compromise that tries to make everything look reasonable, but nothing is perfect.
Choosing the right projection depends on what the map is for. There is no one best way to make a flat map.
5. Hyperbolic Geometry
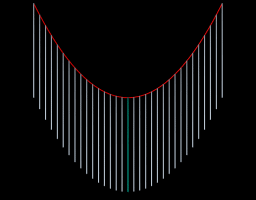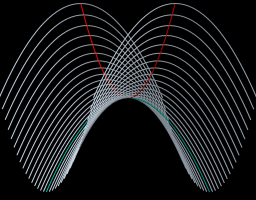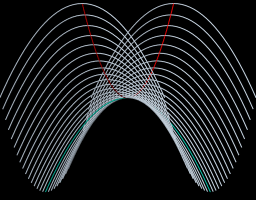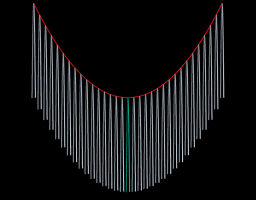
We’ve talked about flat geometry (Euclidean) and spherical geometry (curved like a ball). But there’s another kind: hyperbolic geometry.
In hyperbolic geometry:
- The surface curves the opposite way of a sphere, like a saddle.
- The angles of a triangle add up to less than 180 degrees.
- There are many parallel lines through a single point.
The Earth doesn’t have large areas of hyperbolic geometry, but this kind of geometry is important in math and can help us understand things like map distortions and alternate ways of viewing space.
Some special maps, like the Poincaré disk, use hyperbolic geometry to show infinite spaces in a finite circle. These are useful in computer graphics and art (like M.C. Escher’s famous prints).
6. Topology
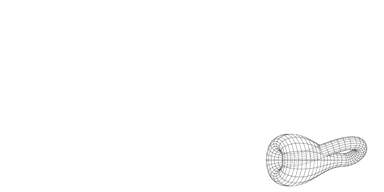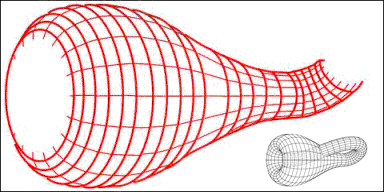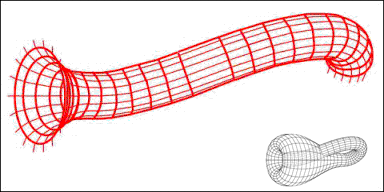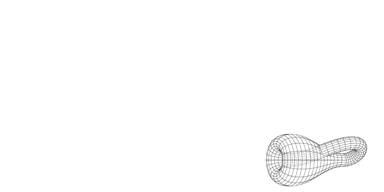
Finally, we come to topology. This is a branch of math that looks at shapes in a very flexible way. In topology, you can stretch, twist, or bend things—as long as you don’t tear or glue them.
From a topologist's view, a donut and a coffee cup are the same, because each has one hole. But a sphere (like the Earth) is different because it has no holes.
Why does this matter for maps? Because topology tells us what is possible and impossible when we try to represent the Earth.
For example, topology tells us:
- You can’t make a flat map of the Earth without some distortion.
- You can cut the Earth into pieces to reduce distortion (like in a globe with flaps).
- You can wrap maps around different shapes (like cylinders or cones) to change how they look.
Topology helps mapmakers think creatively about how to represent the world in different ways.
Conclusion
Making maps is a blend of art and science. It involves deep ideas from mathematics like metric spaces, spherical geometry, projections, and topology. Even riddles like the hunter and the bear can teach us something about how the world works.
So next time you look at a map, remember: you’re not just seeing places. You’re seeing the results of centuries of mathematical thinking, clever ideas, and the challenge of turning a round world into a flat picture.
Maps may look simple, but behind them is a beautiful world of math.
You can learn these concepts and more at Dr Hock's maths and physics tuition.